The Levenshtein distance is a string metric for measuring difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits (i.e. insertions, deletions or substitutions) required to change one word into the other. It is named after Vladimir Levenshtein, who considered this distance in 1965.
Levenshtein distance may also be referred to as edit distance, although it may also denote a larger family of distance metrics. It is closely related to pairwise string alignments.
Definition
Mathematically, the Levenshtein distance between two strings a, b (of length |a| and |b| respectively) is given by leva,b(|a|,|b|) where:
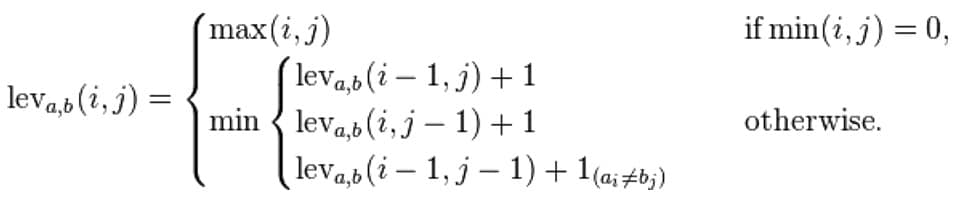
where 1(ai≠bi) is the indicator function equal to 0 when ai≠bi and equal to 1 otherwise, and leva, b(i,j) is the distance between the first i characters of a and the first j characters of b.
Note that the first element in the minimum corresponds to deletion (from a to b), the second to insertion and the third to match or mismatch, depending on whether the respective symbols are the same.
Example
The Levenshtein distance between “FLOMAX” and “VOLMAX” is 3, since the following three edits change one into the other, and there is no way to do it with fewer than three edits:
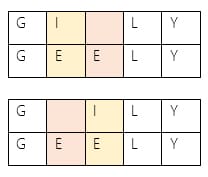
Levenshtein distance between “GILY” and “GEELY” is 2.
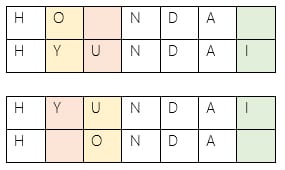
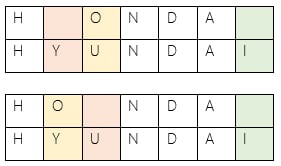
Levenshtein distance between “HONDA” and “HYUNDAI” is 3.
Application
- String Matching.
- Spelling Checking.
Dynamic Programming Approach
The Levenshtein algorithm calculates the least number of edit operations that are necessary to modify one string to obtain another string. The most common way of calculating this is by the dynamic programming approach:
- A matrix is initialized measuring in the (m, n) cell the Levenshtein distance between the m-character prefix of one with the n-prefix of the other word.
- The matrix can be filled from the upper left to the lower right corner.
- Each jump horizontally or vertically corresponds to an insert or a delete, respectively.
- The cost is normally set to 1 for each of the operations.
- The diagonal jump can cost either one, if the two characters in the row and column do not match else 0, if they match. Each cell always minimizes the cost locally.
- This way the number in the lower right corner is the Levenshtein distance between both words.
An example that features the comparison of “HONDA” and “HYUNDAI”,
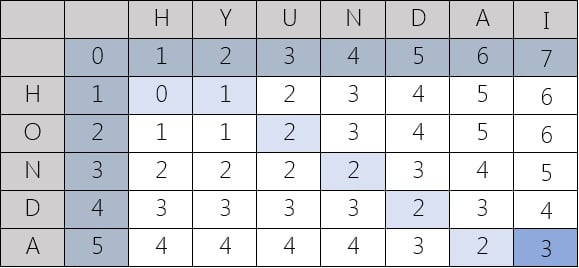
Following are two representations: Levenshtein distance between “HONDA” and “HYUNDAI” is 3.
Use Case
In approximate string matching, the objective is to find matches for short strings in many longer texts, in situations where a small number of differences are to be expected. The short strings could come from a dictionary, for instance. Here, one of the strings is typically short, while the other is arbitrarily long. This has a wide range of applications, for instance, spell checkers, correction systems for optical character recognition and software to assist natural language translation based on translation memory.
The Levenshtein distance can also be computed between two longer strings. But the cost to compute it, which is roughly proportional to the product of the two string lengths, makes this impractical. Thus, when used to aid in fuzzy string searching in applications such as record linkage, the compared strings are usually short to help improve speed of comparisons.
Related Reading
[wcp-carousel id=”10003″]